The Mathematical Reasoning section of the GED tests your ability to solve algebraic and quantitative problems. The goal is to measure your mathematical knowledge and problem-solving skills.
Topics included in this portion of the exam are quantitative and algebraic problem-solving, geometry, data analysis, and data sense. This GED Math reviewer will help you prepare for this important exam.
GED Ready Math reviewer, pt. 3
Direction: Solve each problem and select the best answer. You may use your calculator and use the Mathematics Formula Sheet as needed.
Question 1. What is the value of the smallest number in a series of three consecutive odd integers, if their sum is \(\mathbf{51}\)?
A. 20
B. 19✅
C. 15
D. 12
Question 2. Which of the following points lies on the graph of the equation \(\mathbf{y=2x-3}\)?
A. \((1, 0)\)
B. \((-3, -9)\)
C. \((0, -2)\)
D. \((2, 1)\)✅
For questions 3 and 4 refer to the pie graph provided below.
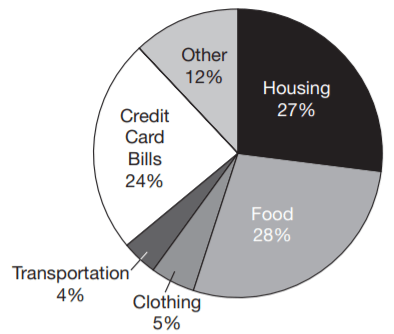
Question 3. What fraction of the Marcy’s monthly take-home pay goes toward clothing?
A. 1/20✅
B. 2/40
C. 3/20
D. 3/50
Question 4. If the Marcy’s monthly take-home pay is $2,500, about how much do they plan to pay each month on their credit card debt?
A. $240
B. $300
C. $450
D. $600✅
Question 5. One number is 5 less than twice another number. The sum of the two numbers is 25. What are the numbers?
A. 10 and 15
B. 8 and 17
C. 12 and 13
D. 7 and 18✅
Question 6. Samson plans to carpet their bedroom and the adjoining hallway as shown in the diagram. What is the area of the bedroom and hallway in square feet?
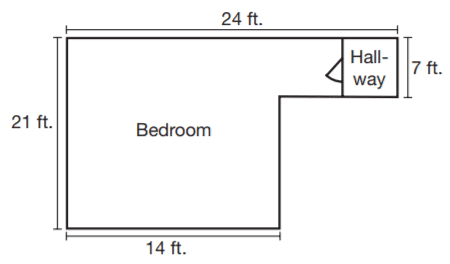
A. 294
B. 336
C. 364✅
D. 504
Question 7. In a right triangle, the hypotenuse measures 10 cm. If one leg of the triangle measures 6 cm, which of the following equations could be used to find the length of the other leg (x) in cm?
A) \(x^2 + 6^2 = 10^2\)✅
B) \(x^2 – 6^2 = 10^2\)
C) \(x^2 + 10^2 = 6^2\)
D) \(x^2 – 10^2 = 6^2\)
Question 8. A cylindrical tank has a radius of 5 feet and a height of 10 feet. What is the volume of the tank in cubic feet?
A. 1000π cubic feet
B. 750π cubic feet
C. 500π cubic feet✅
D. 250π cubic feet
Question 9. Classify the figure containing interior angles 3, 6, 11, and 13.
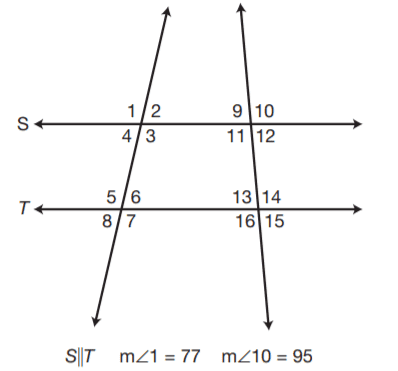
A. parallelogram
B. trapezoid✅
C. square
D. rectangle
Question 10. Two sides of a triangle measure 5cm and 7cm. If the triangle is a right triangle, which of the following could be the measure, in cm, of the third side?
A. 3 cm
B. 8 cm✅
C. 9 cm
D. 12 cm
Question 11. The lengths of the sides of a triangle are 4cm, 7cm, and 9cm. Which of the following conclusions must be true?
A. The triangle is a right triangle.
B. The triangle is an isosceles triangle.
C. The triangle is an equilateral triangle.
D. The triangle is an acute triangle.✅
Question 12. What is the value of the expression \(\mathbf{4(3^2+ 2)-5(2^3-1)}\)?
A. 25
B. 33✅
C. 35
D. 39
Question 13. On a coordinate plane, a vertical line is drawn through the point \(\mathbf{(5,2)}\). On the same plane, a horizontal line is drawn through the point \(\mathbf{(−1,7)}\). At what point on the plane will the two lines intersect?
A. \((−1,2)\)
B. \((5,7)\)
C. \((5,−1)\)
D. \((−1,2)\)✅
For questions 14 and 15 refer to the figure provided below.
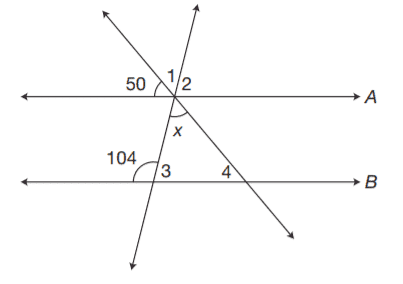
Question 14. What is the value of \(\mathbf{x}\)?
A. 54°✅
B. 76°
C. 126°
D.130°
Question 15. What is the measure of \(\mathbf{\angle4}\)?
A. 130°
B. 120°
C. 50°✅
D. 45°
Question 16. Which of the following is a graph of the inequality \(\mathbf{−2≤x<4}\)?

A. Option A
B. Option B
C. Option C
D. Option D✅
Question 17. On a map, the distance between two cities is 4 and 1/3 inches. The map scale reads 1 inch = 100 miles. What is the actual distance, in miles, between the two cities?
A) 30 miles
B) 400 miles
C) 430 miles✅
D) 433 miles
Question 18. In a swimming competition, the times (in seconds) for six swimmers to complete a 200-meter freestyle race are as follows: 120, 160, 140, 180, 150, and \(\mathbf{x}\). If the median time for the race is 150 seconds, what is the value of x?
A. 140
B. 150
C. 160
D. 170✅
Question 19. Sandy ordered 2 pizzas and 3 sandwiches for a total of $31. The pizzas cost $8 each and the sandwiches cost $3 each. How much did Sandy pay for the pizzas?
A. $8
B. $16✅
C. $24
D. $31
Question 20. To set up a tent, workers place a 25-foot pole in the center of a grassy area as shown in the diagram. A bracing wire is attached to the top of the pole and to a stake 9 feet from the base of the pole. Which of the following represents the length of the bracing wire?
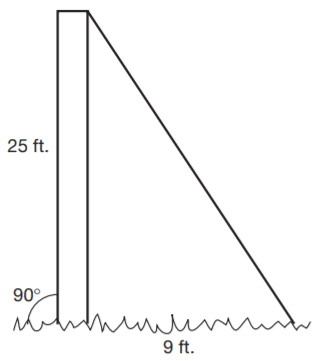
A. \(\sqrt{706}\) ✅
B. \(\sqrt{625}\)
C. \(\sqrt{256}\)
D. \(\sqrt{150}\)
Question 21. The dimensions of Box B, shown below, are twice the length of the corresponding dimensions of Box A (not shown).
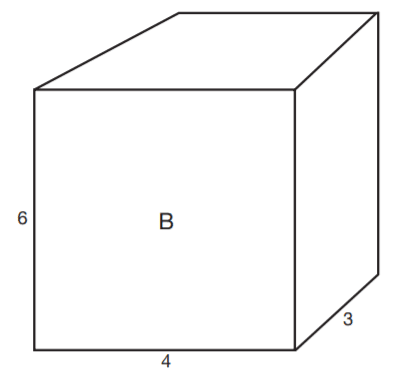
A. The volume of Box B is three times the volume of Box A.
B. The volume of Box B is twice the volume of Box A.
C. The volume of Box B is eight times the volume of Box A.✅
D. The volume of Box A is greater than the volume of Box B.
Question 22. A display of canned soda has a sign that reads “5 cans for $3.” At the same rate, how much would the store charge, to the nearest whole cent, for 8 cans?
A. 1.80
B. 2.80
C. 3.80
D. 8.80✅
Question 23. A restaurant offers a discount on its meals based on the number of people in a group. The function that describes the discount (D) based on the number of people (p) in the group is \(\mathbf{D(p)=0.10p+0.05p^2}\). If a group of 6 people dine at the restaurant, what is the amount of the discount they receive?
A. $0.60
B. $1.20
C. $2.70✅
D. $4.20
Question 24. A rectangle is drawn on a coordinate grid so that two vertices are located at \(\mathbf{(1,3)}\) and \(\mathbf{(7,3)}\), and one side lies along the x-axis. At what coordinates should the other two vertices be located?
A. \((1,7)\) and \((3,7)\)
B. \((1,0)\) and \((7,0)\)
C. \((7,6)\) and \((1,0)\)
D. \((7,0)\) and \((1,6)\) ✅
Question 25. At the end of the school year, 8% of the students at a high school will be graduating. If 48 students are graduating, how many students are enrolled in the high school?
A. 400
B. 500
C. 600✅
D. 700
Question 26. Albert and Lewis decided to share the cost of buying their friends a wedding gift. Albert put in $20 less than twice the amount that Lewis contributed. Together, they spent $94. How many dollars did Albert contribute toward the gift?
A. $56✅
B. $66
C. $76
D. $86
Question 27. What was Joseph’s mean score for a round of golf in August if his scores for each round were 78, 86, 82, 81, 82, and 77?
A. 78
B. 81✅
C. 82
D. 86
Question 28. The three interior angles of ΔJKL measure 45°, 45°, and 90°. The three interior angles of ΔPQR measure 45°, 45°, and 90°. The side JK of JKL measures 4 cm. Based on the given information, which of the following must be a true statement?
A. ΔJKL and ΔPQR are congruent triangles.
B. Δ JKL and ΔPQR are acute triangles.
C. One side of ΔPQR measures 4 cm
D. ΔJKL and ΔPQR are similar triangles.✅
Question 29. A rope, 15 feet long, is cut into four equal pieces. Assuming no waste when the cuts are made, what is the length of each piece?
A. 2 feet 3 inches
B. 3 feet 9 inches✅
C. 5 feet
D. 6 feet 3 inches
For questions 30 and 31 refer to the line graph provided below
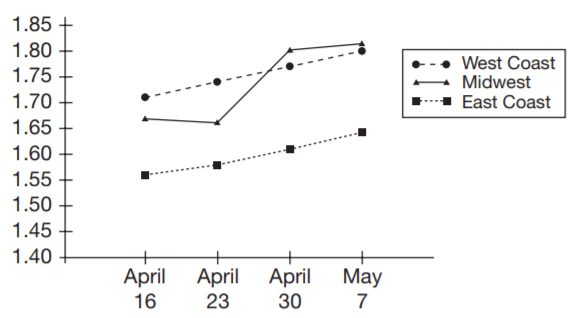
Question 30. On what date and in what location was there the greatest jump in the price of gasoline from one week to the next?
A. April 30 in the Midwest✅
B. April 30 on the West Coast
C. May 7 in the Midwest
D. May 7 on the East Coast
Question 31. Based on the information in the graph, which of the following is the best prediction of the price per gallon of gasoline on the West Coast for the week following May 7?
A. $1.64
B. $1.82✅
C. $1.80
D. $1.90
Question 32. In quadrilateral ABCD, side AB is parallel to side CD. Sides AD and BC are not parallel. What is the area of the figure to the nearest square centimeter?
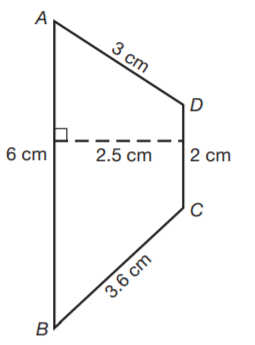
A.12 cm²
B.14 cm²
C.10 cm²✅
D.18 cm²
Question 33. A bag contains 12 red, 3 blue, 6 green, and 4 yellow marbles. If a marble is drawn from the bag at random, what is the probability that the marble will be either blue or yellow?
A. 28%✅
B. 25%
C. 20%
D. 15%
Question 34. The Smithville High School basketball team won 12 games and lost 6 games this season. What is the ratio of games won to games lost?
A. 6:12
B. 1:2✅
C. 2:1
D.12:6
Question 35. Jared bought a used car for $10,000. He spent an additional $2,500 replacing the brakes, tires, and spark plugs. He then sold the car for 20% more than what he paid for it. For what amount, in dollars, did Jared sell the car?
A. $10,000
B. $12,000
C. $12,500
D. $14,500✅



